Penghitungan Surplus production dengan asumsi non-equilibrium menggunakan data fitting

Penggunaan montiR diawali dengan penyediaan data yang meliputi data tahun, data tangkapan serta data catch per unit effort yang dibuat dalam dataframe. Berikut adalah contoh untuk membuat dataframe sebagai input untuk analisis montiR menggunakan data tangkapan Yellowfin Tuna di East Pacific (Schaefer, 1957).

df <- data.frame(year=c(1934:1955),
                 catch=c(60913,72294,78353,91522,78288,110417,114590,76841,41965,50058,64094,
                        89194,129701,160134,200340,192458,224810,183685,192234,138918,138623,140581),
                 cpue=c(10361,11484,11571,11116,11463,10528,10609,8018,7040,8441,10019,9512,9292,
                        7857,8353,8363,7057,9809,6097,3814,5546,7895))

Pada tahap ini diharapkan data catch per unit effort sudah melalui langkah data standardization yang idealnya diolah dengan analisis menggunakan Generalized Linear Model.

a. Data plotting

Langkah paling penting sebelum melakukan analisis adalah memeriksa apakah data yang akan digunakan memenuhi persyaratan dan asumsi yang dibutuhkan untuk analisis biomass dynamic model, termasuk memilih jenis langkah apa yang harus dilakukan ketika data yang dibutuhkan tidak memenuhi asumsi. Para ahli statistik dan pemodelan matematik selalu memulai analisisnya dengan, “Plot your data!”.

Langkah untuk melihat grafik jumlah tangkapan (catch), upaya (effort) serta catch per unit of effort (CPUE)/indeks kelimpahan dari data yang dimiliki dapat dilakukan dengan mudah menggunakan kode dan contoh data yang tersedia sebagaimana berikut:

plotInit(df=df.goodcontrast0)
plotInit(df=df.onewaytrip0)

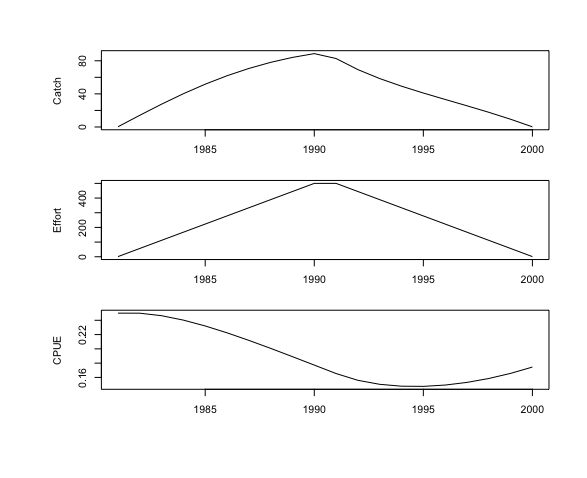
Disini kita akan melihat dua jenis data yang biasanya terdapat pada perikanan, goodcontrast dan onewaytrip. Biomass dynamic model dengan menggunakan metode data fitting mensyaratkan data yang memiliki kontras yang cukup pada Catch per Unit Effort (CPUE), ditunjukkan dengan adanya kontras data yang baik (i.e. memiliki representasi pola turun dan naik) serta paling tidak memiliki 20 tahun entry untuk tangkapan dan upaya (Punt & Hilborn, 1996; Magnusson & Hilborn, 2007). Contoh dari data yang memiliki kontras yang cukup dapat dilihat pada df.goodcontrast0 dan df.namibianCatch, dimana contoh plot dari df.goodcontrast0 dapat dilihat berikut:

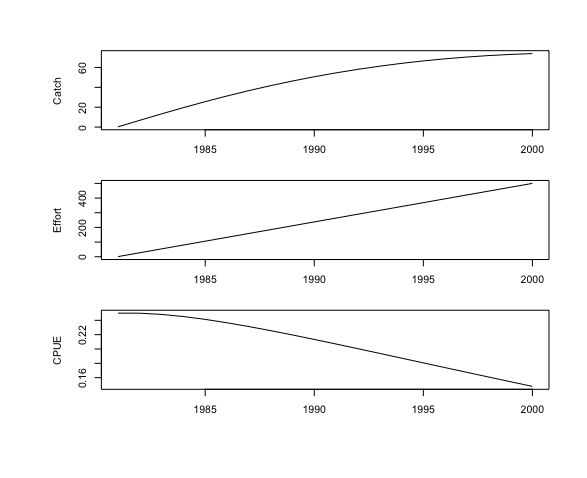
Contoh data yang tidak memiliki kontras yang baik dapat dilihat pada df.onewaytrip0 dan df.eastpacCatch. Dapat dilihat bahwa data tangkapan dan upaya memiliki pola meningkat dengan tidak memiliki pola menurun sebagaimana yang ditunjukkan dari plot df.onewaytrip0 berikut:

Grafik berikut menunjukkan pentingnya jumlah dan jenis data yang memiliki kontras serta bagaimana tipe data memerlukan metode analisis yang berbeda pula. Disini tersedia contoh menggunakan simulasi dengan 2000 ulangan untuk menghitung MSY, dimana idealnya analisis akan menghasilkan angka 50. Dapat dilihat pada panel sebelah kiri bahwa data yang memiliki kontras yang baik dengan runtun waktu sebanyak 20 tahun atau lebih akan menghasilkan akurasi yang lebih baik di seputar angka 50, berbeda halnya dengan data runtun waktu 10 tahun yang menghasilkan deviasi lebih tinggi. Ketika menggunakan data dengan tipe one-way trip sebagaimana pada panel sebelah kanan, dapat dilihat bahwa metode data fitting biasa akan menghasilkan akurasi analisis yang melenceng jauh meskipun menggunakan jumlah data yang cukup. Selain penting untuk menggunakan metode yang tepat sesuai dengan tipe data yang ada, penting untuk menghitung standard error dan atau confident interval dari hasil analisis.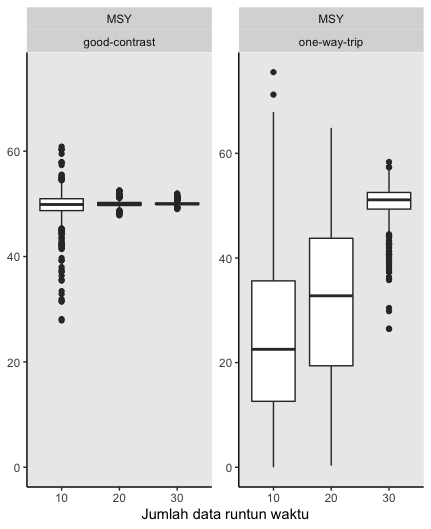

Jenis data yang berbeda harus dianalisis menggunakan cara yang berbeda pula. Hal ini akan dijelaskan lebih lanjut di bagian selanjutnya.

b. Estimasi parameter surplus production dengan data fitting

Tool ini melakukan estimasi parameter K, B0, r, q dan menentukan jumlah tangkapan ikan lestari (MSY), biomassa ikan lestari (Bmsy), serta upaya penangkapan ikan lestari (Emsy) menggunakan data runut waktu dengan asumsi non-equilibrium untuk model Schaefer.

Proses estimasi diawali dengan mencari angka awal yang diperkirakan sesuai dengan parameter K, B0, r, q. Hal ini dilakukan dengan menduga angka parameter, kemudian dilihat apakah grafik yang dihasilkan dari parameter yang kita duga memberikan grafik yang sesuai dengan data yang akan kita lakukan pendugaannya. Misalnya kita akan menduga parameter surplus production dari data df.namibianCatch, maka cara estimasinya dilakukan dengan mencari angka awal terlebih dahulu hingga menghasilkan garis observation dan estimation yang fit.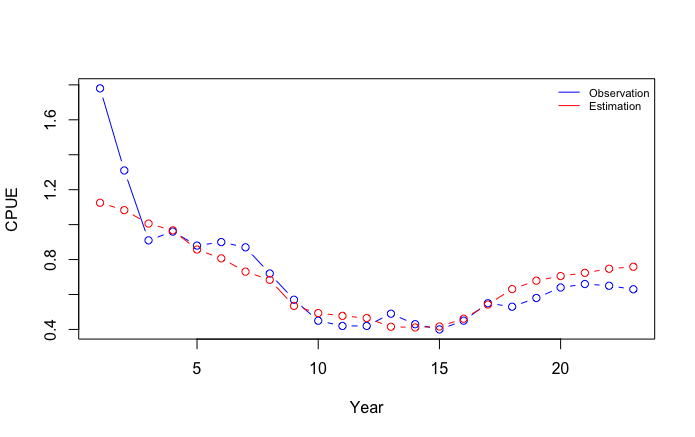

Mencari angka awal ini dilakukan dengan merubah angka K, r dan q sehingga dirasa grafik hasil dari angka awal (Estimation) dirasa sudah sesuai (fit) dengan data yang akan kita analisis (Observation). Sebagai panduan pada tahapan ini, angka K berada pada kisaran 3 hingga 15 kali angka maksimal tangkapan, angka B0 diset sama dengan K, angka r seharusnya berada pada rentang antara 0-1.3 sesuai spesies ikan dan angka q biasanya berada pada rentang antara 0-0.01.

library('montiR')

K <- 2500
B0 <- 2500
r <- 0.46
q <- 0.00045

inpars <- c(K, B0, r, q)
Par_init(inpars=inpars, df=df.namibianCatch)

Parameter pertumbuhan intrinsik r memiliki nilai yang spesifik sesuai dengan jenis ikan (Adams, 1980; Kawasaki, 1980, 1983). Fishbase dan SeaLifebase telah mengumpulkan angka r untuk mayoritas spesies akuatik dan dapat digunakan untuk membantu dalam proses estimasi parameter. Angka pertumbuhan intrinsik ini dapat dicari secara manual dengan membuka website dua database ini secara langsung. Jika memiliki akses internet, dapat juga langsung mencari kisaran angka r ini dengan mencari melalui rGrabber(NamaSpesies) dengan terlebih dahulu mengaktifkan package rfishbase. Setelah menjalankan kode tersebut dapat dilihat bahwa ikan Hake Namibia yang memiliki nama ilmiah Merluccius capensis ini memiliki nilai r sebesar 0.2525 dengan rentang 0.0005-0.5 yang dihasilkan dari informasi resiliensi spesies, dimana angka r sebesar 0.46 pada input diatas masih berada pada rentang yang disarankan.

Setelah angka awal didapat, maka langkah selanjutnya adalah melakukan optimasi parameter melalui Maximum Likelihood Estimation dengan observation error. Observation error menggunakan asumsi bahwa terdapat kesalahan pada hubungan antara biomass dan indeks kelimpahan, sehingga parameter ini perlu untuk diestimasi. Indeks kelimpahan diasumsikan mengikuti distribusi log-normal untuk melakukan estimasi parameter K, B0, r, q dan sigma (observation error).

Proses estimasi parameter dilakukan menggunakan data df.goodcontrast dengan langkah sebagai berikut:

library('montiR')

calc.MSY(K=1000,
         B0=1000,
         r=0.2,
         q=0.00025,
         s.sigma=0.1,
         df=df.goodcontrast,
         plot=TRUE)

Setelah input diatas dijalankan, akan dihasilkan estimasi parameter K, B0, r, q dan observation error beserta estimasi MSY, upaya pada MSY, Biomass pada MSY serta tingkat pemanfaatan pada MSY dan tingkat pemanfaatan pada upaya optimal ketika MSY sebagai berikut:

$Parameter
    SPpar  fitted_pars
1       K 1.101868e+03
2      B0 1.090818e+03
3       r 1.689499e-01
4       q 2.238730e-04
5 s.sigma 4.380054e-02

$MSY
       MSY     Emsy     Bmsy E.rate_MSY E.rate_Emsy
1 46.54015 377.3343 550.9342  0.3514896  0.04335249

Ketika plot=TRUE, maka secara otomatis akan ditampilkan grafik hasil dimana garis estimation (warna merah) akan fit dengan garis data observation (warna biru).

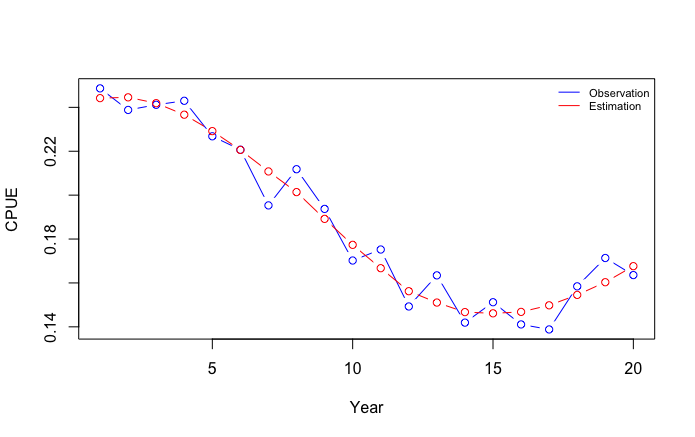
Data frame $Parameter menyimpan angka estimasi hasil optimasi (fitted_pars). Sebagai panduan untuk memeriksa hasil parameter, angka K biasanya selalu lebih tinggi dibanding B0, angka r seharusnya berada pada rentang antara 0-1 dan angka q biasanya berada pada rentang antara 0-0.01.

Jika angka hasil optimasi masih belum sesuai dengan panduan sederhana ini, maka ada dua hal yang dapat diperiksa (i) kemungkinan input kurang sesuai, atau (ii) data kurang sesuai untuk dilakukan optimasi dengan cara biasa sehingga perlu penambahan constrain. Untuk kasus kedua, proses optimasi dapat dilakukan secara manual dengan angka awal dibatasi menggunakan batas bawah (lower) dan batas atas (upper) serta merubah metode optimasi menjadi “L-BFGS-B”. Penggunaan constrain seperti yang dilakukan dibawah ini membutuhkan pemahaman tentang perkiraan jumlah stok sehingga perlu dilakukan dengan hati-hati untuk dapat menghasilkan estimasi yang akurat.

inpars <- c(log(K), log(B0), log(r), log(q), log(s.sigma))

fit <- optim(par = inpars,
             fn = Par.min,
             df = df.goodcontrast,
             method = "L-BFGS-B",
             lower = xxxx,
             upper = xxxx
 )

 vals <- exp(fit$par)
 res <- data.frame("SPpar" = c("K", "B0", "r", "q", "s.sigma"),
                   "fitted_pars" = vals)
 res

Untuk data yang memiliki tipe one way trip, input yang digunakan dalam optimasi perlu disesuaikan terlebih dahulu. Penjelasan lebih lanjut untuk metode ini akan ditulis beberapa waktu kedepan. Selain itu, tool ini sudah disesuaikan untuk kebutuhan data yang terbatas (dapat mengakomodasi hilangnya sedikit input data upaya penangkapan).

c. Menghitung standard error dan confidence interval dari reference point

Tool ini mengestimasi jumlah stok ikan yang lestari (Bmsy), jumlah tangkapan ikan lestari (MSY) dan upaya penangkapan ikan lestari (Emsy) serta menghitung standard error menggunakan data runut waktu dengan asumsi non-equilibrium untuk model Schaefer.

Penghitungan standard error dari reference point dapat dilakukan dengan menggunakan output dari analisis sebelumnya sebagai input untuk analisis berikut

library(montiR)

calc.SE(MSY=46.54015,
        Emsy=377.3343,
        Bmsy=550.9342,
        s.sigma=4.380054e-02,
        df=df.goodcontrast)

Setelah kode diatas dijalankan, akan dihasilkan estimasi parameter untuk Bmsy, MSY, Emsy dengan perhitungan standard error-nya. Untuk kebutuhan pengelolaan, dipersilahkan untuk menggunakan parameter yang dihasilkan berikut:

  ManagPar  fitted_pars      std_err
1     Bmsy  46.54049070  3.063154812
2      MSY 377.33435477 25.400928220
3     Emsy 545.53973460 47.890948600
4    sigma   0.04392642  0.006966182

Selain itu, dapat juga dihitung rentang kepercayaan dari MSY dengan metode profile likelihood. Penghitungan ini dilakukan dengan memasukkan angka MSY dan r dari perhitungan sebelumnya:

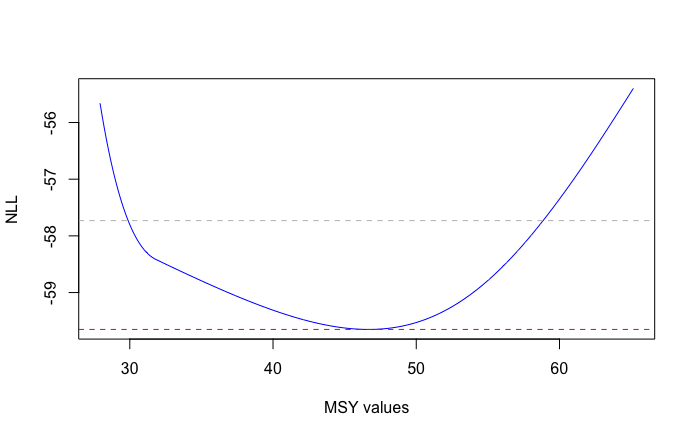
calc.CI(MSYval=46.54015,
        rval= 1.689499e-01,
        df=df.goodcontrast,
        plot=TRUE)

yang akan menghasilkan angka terbaik dugaan untuk MSY serta 95% rentang kepercayaan dari angka MSY tersebut. Dimana angka MSY dihitung dan memiliki rentang bawah dan atas sebagaimana dibawah

       MSY  lowerCI  upperCI
1 46.67059 29.89937 58.82041

Bisa dilihat pada gambar dibawah dimana nilai terbaik MSY menyentuh garis merah, kemudian rentang kepercayaan bagian bawah dan atas menyentuh pada grais abu-abu di sebelah kanan dan kiri kurva.